Реверс ELF`а c большими buffer`ами c TU CTF 2016

В прошедшем TU CTF было несколько задач категории Reverse.

Таск на 350 баллов(Holy Grail).
Дан ELF, про который ничего не говорится...

Для начала проведем первичный анализ - что может сказать утилита анализа заголовков:



Ничего такого, за исключением того, что этот бинарник собирался на 64-разрядной платформе и для нее же предназначен.
Значит сразу же отметаем в сторону 32-битные анализаторы.

IDA позволила оценить внутреннюю структуру бинарника (точка входа - main):



Очевидно, что приложение было написано на C++, т.к используются стандартные потоковые классы, ловко восстановленные в псевдокод плагином иды HexRays.

Замечаем парочку примечательных функций, в которые передается введенный пароль - validChars() и stringMod().
Дабы не тянуть время, скажу, что первая из них тупо проверяет ввод - в нем должны быть строго ASCII символы в диапазоне кодов [65..122] - т.е буквы ONLY: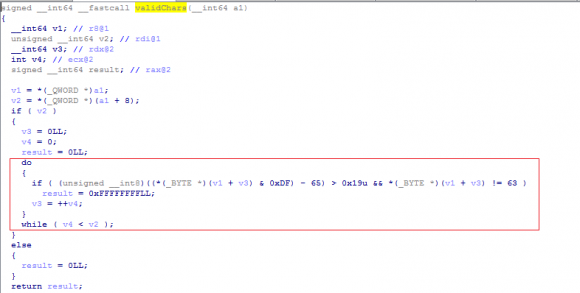



Если функция возвратит отрицательное число(интерпретация boolean: -1 или 0), то прыгаем посредством метки в фейл-зону. Dead End.
Поэтому теперь знаем, что вводить можно только буквы.

Метод stringMod с говорящим названием: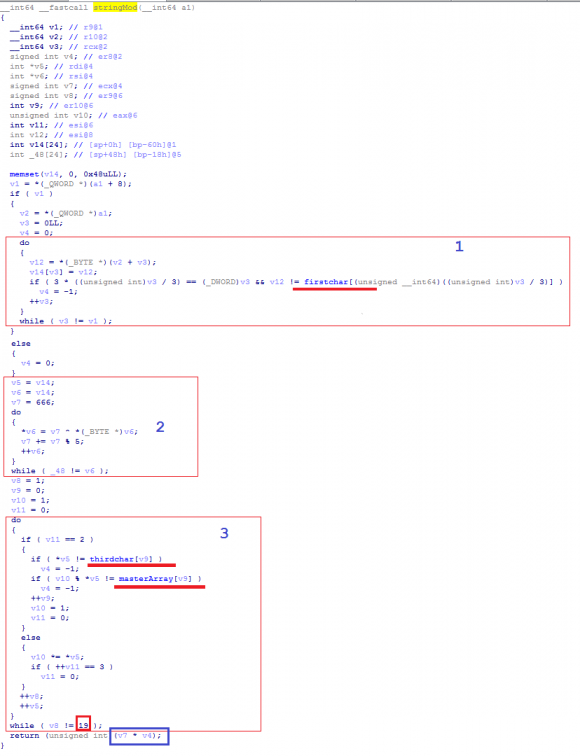



Метод сокрытия пароля выглядит довольно муторно. И правда, чтобы со всем здесь разобраться, потребовалось почти 2.5 часа.
Здесь я красным выделил блоки, которые являются этапами "раскрытия" пароля. Таких этапов 3.

Начинать решение, пожалуй, как и любой другой сложной задачи стоит с конца. Что возвращает функция? Из примера "реконструкции" validChars() мы уже знаем, что это изощренный прототип boolean. True - это когда возвращается 0, а False - (-1)(0xffffff). Также можно видеть, что значение v7 никогда не будет равно 0, а значит единственный способ заставить функцию естественным образом вернуть истину - обратить v4 в 0.
Кроме того можно увидеть, что пароль состоит из 18(19-1) символов.

В красных блоках можно видеть условия, при которых v4 обращается в Ложь.
Начинаем с первого блока. Условие, которое выполняется на каждой итерации цикла имеет следующую суть: если номер итерации(v3) кратен 3(0..3..6..) и символ пароля(v12 - переменная с девственным паролем) в позиции [v3] НЕ равен символу из буффера firstchar, то обращаем результат в Ложь(v4=-1).

Нужно этого избежать! Для этого каждый 3 символ(включая нулевой) должен совпадать с символом из буфера firstchar.
А что в firstchar? Это статичная область данных, находящихся в секции данных:



Всего 8 байт, но мы уже знаем, что пароль состоит из 18 символов, а тут сверяется каждый третий -> нужны первые 6 символов.

Имеем 1/3 восстановленного пароля:  A..i..n..e..o..a..

Переходим ко 2 красному блоку

Там мы видим, что каждый байт пароля циклично XOR`ится(куда же без ксора!) на число дьявола с прибавлением остатка от деления по модулю 5.



Это немножко усложнило задачу, но не сильно.

Переходим к 3 блоку.

Здесь "раскрываются" 2 и 3 байты в каждом трио(трайте?) байт-связок. Логика блока: последовательно пройтись по всем символам введенного пароля, инкрементируя счетчик и перемножая значения байт 1 и 2 байта из байта-связки(трио байт) в переменную v10. Если счетчик кратен двум, то проверяем сначала значение третьего байта связки(thirdchar).

Thirdchar, как и firstchar - это ресурсы, являющиеся статикой:



Тут стоит помнить о двух вещах: 1) значения по`XOR`ены на цикличный прирост к 666. 2) О порядке представления байт в памяти - Little Endian(обратный порядок байт), что означает, что красная "2" перетекает в старший байт(замещает 0).

Вытащив буфер thirdchar(0x2EF, 0x2C4, 0x2DC, 0x2C7, 0x2DE, 0x2FC) и пре`XOR`ив его на (669, 673...), получаем реконструированные третьи байты флага.

Уже имеем 2/3 восстановленного флага:  A.ri.an.re.ro.ea.?

Можно заметить появление знака вопроса(когда разрешен ввод лишь букв), но дело в том, что самый последний символ не проходи проверку на validChars().

Осталось восстановить средние байты в трио байт-связок. Это самый муторный этап, посмотрите еще раз:



Вычисления каждого второго символа основано на байт-произведении первого и второго символов трио, разделенных по модулю на байт-значение третьего. Можно составить несложное уравнение, ведь 3 из 4 элементов уравнения нам известны.
Вот буффер masterArray из секции ресурсов:



Опять же, порядок - Little Endian(старший разряд байта в минимальной по адресу ячейке памяти)!
Вот пример уравнения для первого трио на псевдокоде:



Теперь осталось решить 6 таких уравнений, чтобы получить все вторые байты в трио байт. Не забываем, что в этом уравнении все компоненты по`XOR`ены на циклический сдвиг числа дьявола.

Пример брута(лень решать их в уме/на листочке) уравнения(для первого трио байт) с помощью скрипта на Python:

for i in range(65,123):
	for j in range(65,123):
		if( ((ord('A')^666) * i^667 ) % (ord('r')^669) == 0x1D7 ):
			print(chr(i));

Далее будут меняться только "производные" числа дьявольского числа(в соответствии с алгоритмом приращения, описанным выше) и символы, "окружающие" i - второй байт.

Таким образом вытащили из masterArray информацию о вторых символах байт-связок:


Вставляем их в

2/3 восстановленного флага:  A.ri.an.re.ro.ea.?

и получаем флаг:

tuctf{AfricanOreuropean?}

Убеждаемся в труЪшности решения:



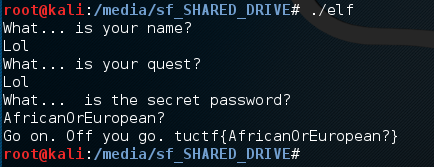
Profit!!11скачать dle 10.5фильмы бесплатно