Twin Primes writeup

Райтап от swani по таску Twin Primes (криптография)

В задании дан 7z архив (twin-primes.7z [1,37 Kb] (cкачиваний: 12) ).




Открыв который мы видим скрипт на питоне, зашифрованный текст и два файла (key1, key2).




Откроем скрипт.

 from Crypto.Util.number import *
import Crypto.PublicKey.RSA as RSA
import os

N = 1024

def getTwinPrime(N):
    while True:
        p = getPrime(N)
        if isPrime(p+2):
            return p

def genkey(N = 1024):
    p = getTwinPrime(N)
    q = getTwinPrime(N)
    n1 = p*q
    n2 = (p+2)*(q+2)
    e = long(65537)
    d1 = inverse(e, (p-1)*(q-1))
    d2 = inverse(e, (p+1)*(q+1))
    key1 = RSA.construct((n1, e, d1))
    key2 = RSA.construct((n2, e, d2))
    if n1 < n2:
        return (key1, key2)
    else:
        return (key2, key1)

rsa1, rsa2 = genkey(N)

with open("flag", "r") as f:
    flag = f.read()
padded_flag = flag + "\0" + os.urandom(N/8 - 1 - len(flag))

c = bytes_to_long(padded_flag)
c = rsa1.encrypt(c, 0)[0]
c = rsa2.encrypt(c, 0)[0]

with open("key1", "w") as f:
    f.write("%d\n" % rsa1.n)
    f.write("%d\n" % rsa1.e)
with open("key2", "w") as f:
    f.write("%d\n" % rsa2.n)
    f.write("%d\n" % rsa2.e)

with open("encrypted", "w") as f:
    f.write("%d\n" % c)

Видим, что шифрование RSA. Флаг переводится в long, шифруется ключом key1, затем то, что получилось, шифруется ключом key2. Очевидно, что расшифровывать будем в обратном порядке.

Открываем файл key2:

 19402643768027967294480695361037227649637514561280461352708420192197328993512710852087871986349184383442031544945263966477446685587168025154775060178782897097993949800845903218890975275725416699258462920097986424936088541112790958875211336188249107280753661467619511079649070248659536282267267928669265252935757418867172314593546678104100129027339256068940987412816779744339994971665109555680401467324487397541852486805770300895063315083965445098467966738905392320963293379345531703349669197397492241574949069875012089172754014231783160960425531160246267389657034543342990940680603153790486530477470655757947009682859

Перед нами число N=p*q. Раскладываем его на множители, проделываем аналогичную операцию с N из файла key1.

И так, все что нужно для расшифровывания у нас есть.
Запускаем небольшой скрипт с p и q из key2:

 #!/usr/bin/python2
import gmpy2

p =  109839168287920364771652233739542245893972429420400471787477887103169099491804762856071669374751286279860451783039232642710981517010937585802203565874477414469934412741906018847402147404957765188018616912003220542453809516059524224015255036266232001320821428611494617812180060212800300789614856560253120304703
q =  176645945799298135110721766377313792982812334295271987596634864064777954683139799946630491521527848390622912482826980130051166690303653228530141163053890146954290070312482492552495214917023922382112893625586133272913759418717134953590760109002220865007673751773346439753002517112721944238066505389966935631253
e =  65537
c =  7991219189591014572196623817385737879027208108469800802629706564258508626010674513875496029177290575819650366802730803283761137036255380767766538866086463895539973594615882321974738140931689333873106124459849322556754579010062541988138211176574621668101228531769828358289973150393343109948611583609219420213530834364837438730411379305046156670015024547263019932288989808228091601206948741304222197779808592738075111024678982273856922586615415238555211148847427589678238745186253649783665607928382002868111278077054871294837923189536714235044041993541158402943372188779797996711792610439969105993917373651847337638929
t = (p-1)*(q-1)
n = p*q

# returns d such that e * d == 1 modulo t, or 0 if no such y exists.
d = gmpy2.invert(e,t)

# Decryption
m = pow(c,d,n)
print "Solved ! m = %d" % m

Получаем Solved !

 m = 373239553115651827369899427657360875834152089860180257161642938987416643279267796017763035136285792087924995986378489367185662378937141758836872403737173549717715557150143694357419301981698777842368254230548612496956689640236300513429314367185641895908387283782093980735699566557226166228162186948786794187770887804007641846622887840125971336743542918133130483166950694027240609779212376907420023775526598867122524264065496089993260728922693481442936815735645015670821959440660673801457483695677241321385338513678687427587288462960873117726647186048326364254058577838850975109848822071400003734396085552080839412313

Запускаем этот же скрипт с p и q, полученными из key1, не забываем менять с на m, который получили на предыдущем шаге. Получаем:

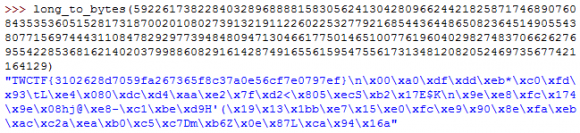
Solved ! m = 59226173822840328968888158305624130428096624421825871746890760843535360515281731870020108027391321911226022532779216854436448650823645149055438077156974443110847829297739484809471304661775014651007761960402982748370662627695542285368162140203799886082916142874916556159547556173134812082052469735677421164129

Не забываем, что перед шифрованием флаг перевели в long. Делаем обратную операцию:

скачать dle 10.5фильмы бесплатно